Matemática elementar/Progressões/Progressão aritmética

Uma progressão aritmética (1,3,5,7).

Progressão aritmética (PA) é uma sequência que tem entre um elemento e seus adjacentes uma diferença igual. Ou seja, uma sequência para a qual se determinam os números somando ou subtraindo a razão de progressão.

Exemplo:

$P=(2,4,6)$

$(6-4=2;4-2=2)$

No exemplo, 2 é a razão de progressão da PA.

Fórmula do termo geral

Denomina-se fórmula do termo geral a uma equação que expressa a regra para obterem-se os elementos da progressão. É praticamente o mesmo que a função que define a sequência. No caso das progressões aritméticas, a fórmula do termo geral é:

$a_n=a_1+(n-1)r$

Onde:

• a_n é o termo que se procura encontrar (n é o índice, por exemplo, a₃ é o terceiro termo da progressão);
• a₁ é o primeiro termo da progressão. Conquanto a fórmula do termo geral seja expressa em função do primeiro termo, nada impede que se utilizem outras posições na sequência, desde que se adapte a fórmula;
• r é a razão de progressão;
• n é, como já explicado, o índice do elemento procurado (a localização do termo na sequência).

Soma dos termos

A soma dos termos de uma PA (S_n), é obtido por:

$S_n=a_1+a_2+a_3+...+a_n$

Considerando a₁ e a_n como o primeiro e o último termo da progressão. Mas imagine a soma de uma progressão de cem termos. Seria bastante demorado somar cada termo para se obter o resultado.

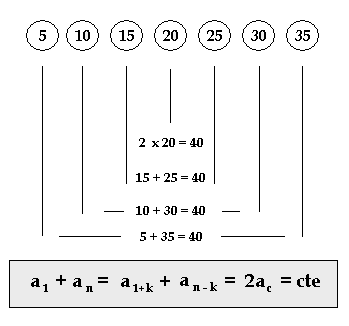
Diz a lenda que o matemático Gauss descobriu uma fórmula prática de soma de termos de uma PA quando tinha cinco anos. Gauss teria sido submetido a um exercício que consistia em somar os números naturais de 1 a 100, e o teria resolvido em alguns minutos, ao contrário do que esperava seu mestre. O diagrama, abaixo, esquematiza o raciocínio de Gauss, em que a soma do primeiro e do último termo equivale a soma do segundo e do penúltimo termo, assim sucessivamente.

Lendas matemáticas à parte, a soma dos termos de uma progressão aritmética pode ser obtida por uma fórmula simples:

$S_n=\frac{(a_1+a_n)n}{2}$

Onde:

• S_n é a soma dos termos até n.
• a₁ e a_n são, respectivamente, o primeiro e o último termo da progressão (ou pelo menos, do subconjunto da progressão sobre o qual será feita a soma)
• n é o total de elementos somados; reparar que a fórmula só permite somar elementos contíguos da progressão

Somatórios

Para uma melhor representação da soma dos termos de uma progressão, foi definido o somatório. No somatório, que é designado pela letra sigma maiúscula, os valores de uma PA são descritos pela seguinte maneira:

$S_n=\sum _{i=0}^n(a_1+ir)$

Por este somatório, é obtido o seguinte resultado:

$\sum _{i=0}^n(a_1+ir)=a_1+a_2+a_3+...+a_n$

Em que:

• n é a quantidade de termos da soma (não necessariamente todos os termos da progressão);
• a_n é o último termo da soma;
• i = 0 é o coeficiente de r para o primeiro termo da soma (igual a a_n - 1), e a cada termo sucessivo que i aparecer, será adicionado 1 ao seu valor;
• r é a razão.

Desta forma, a soma dos 5 termos de uma progressão aritmética, em que o primeiro termo é igual a -7 e a razão igual a 2, teremos:

$\sum _{i=0}^5(-7+2i)=a_1+a_2+a_3+a_4+a_5$

$\sum _{i=0}^5(-7+2i)=(-7+2\times 0)+(-7+2\times 1)+(-7+2\times 2)+(-7+2\times 3)+(-7+2\times 4)$

$\sum _{i=0}^5(-7+2i)=-7+(-5)+(-3)+(-1)+1=-15$