Introdução à física/Estática/Equilíbrio dos corpos rígidos

Predefinição:TOC-direita Quando as forças que agem num corpo são nulas, diz-se que o corpo está equilibrado. Nesses casos, há ausência de aceleração, e consequentemente, o corpo não gira em torno de si. Logo, corpos em equilíbrio satisfazem a seguinte equação:

$\sum M_H=\sum M_{AH}$

Onde M_H é a soma das forças que empurram o corpo para o sentido horário (momento horário) e M_AH, as que empurram para o sentido anti-horário (momento anti-horário). Para calcular cada força individualmente, deve-se desenvolver a equação acima:

$\sum M=M_1+M_2+M_3+...+M_n$

Onde:

$M=F\times d$

Em que:

• M é o momento, em newtons por metro (N/m);
• F a força, em newtons (N);
• d a distância entre um apoio e a força em questão, em metros (m).

No teorema de Lammy:
$\frac{F_1}{\sin {\theta }_1}=\frac{F_2}{\sin {\theta }_2}=\frac{F_3}{\sin {\theta }_3}$

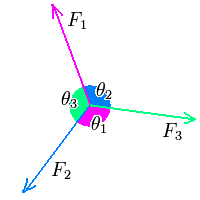
Estática do ponto material

Quando há duas forças atuando sobre um corpo que está em equilíbrio, deve-se fazer a decomposição de vetores, considerando a soma dos momentos igual a zero. Quando há três forças, o melhor método é o teorema de Lammy. Quando há mais de três forças, deve-se fazer a decomposição por fórmulas conjuntas (neste último, R = 0).

Demonstração

a) Um objeto de 1kg encontra-se em equilíbrio em uma rampa que forma ângulo de 30° com a superfície. Qual o coeficiente de atrito que há na rampa? Considere a aceleração gravitacional no local igual a 10 m/s².

• Como o objeto está em equilíbrio, os momentos são de igual intensidade. Assim, a força de atrito deve ser igual à força peso. Deve-se, ainda, decompor os vetores:

$\sum M_H=\sum M_{AH}\to F_{at}=P\sin \theta \to N\mu =P\sin \theta \to mg\mu \cos \theta =mg\sin \theta$

• Substituindo-se por números:

$8,6\mu =5\Rightarrow 0,57N.m$

b) Duas cordas ideais (A e B) presas a um teto plano, dispostas 75° uma da outra, prendem uma luminária L, de 2kg, que se encontra em equilíbrio. A luminária e a corda A formam ângulo de 135°. Qual a tração imposta em cada corda, considerando g = 10 m/s²?

$\frac{20}{\sin 75}=\frac{A}{\sin (360-135-75)}=\frac{B}{\sin 135}$

• Considerando A:

$\frac{A}{0,5}=20,7\Rightarrow 10,35N$

• E considerando B:

$\frac{B}{0,7}=20,7\Rightarrow 29,28N$

Corpos extensos sobre um apoio

Nesses casos, o(s) corpo(s) está(ão) em equilíbrio sobre um apoio.

Demonstração

a) Uma gangorra de quatro metros, homogênea e de massa despresível, é sustentada por um apoio, exatamente a dois metros das extremidades. Uma criança A de massa 30kg está sentada a 2 metros do apoio da gangorra, e uma criança B de massa 40kg está sentada há 1,5 metros do apoio. A gangorra está em equilíbrio, considerando a aceleração gravitacional 10 m/s²?

• Primeiramente, deve-se verificar cada momento. Enquanto a criança A leva a gongorra a girar a um lado, a criança B leva ao outro. Temos então:

$M_A=M_B\to F_A{d}_A=F_B{d}_B$

• Como a força que gera o movimento é a força peso:

$P_A{d}_A=P_B{d}_B$

• Substituindo por números:

$30\times 10\times 2=40\times 10\times 1,5\to 600=600$

Logo, a gangorra está em equilíbrio.

b) Em um salão de festas, há uma mesa de seis metros, sustentada por um apoio localizado exatamente a 3,5 metros da extremidade esquerda, homogênea e de massa A. À esquerda do apoio, há vários objetos: um objeto B de 2kg, localizado a 1,5 metro do apoio e um objeto C de 1kg, a 2 metros. A 1,5 metro do apoio, à direita, está localizado um objeto D, de massa 10kg. Qual a massa da mesa (A), considerando que a mesa está em equilíbrio? Considere g = 10 m/s. Observe que o centro de gravidade da mesa, está situado à esquerda do apoio, logo, as forças A, B e C são do momento da esquerda, e a força D da direita:

$M_{esquerda}=M_{direita}\to 10(A{d}_A+B{d}_B+C{d}_C)=10D{d}_D$

• Substituindo-se por números:

$(10A\times 0,5)+(20\times 1,5)+(10\times 2)=100\times 1,5\to 5A+50=150$

• Então:

$5A=100\to A=20$

Corpos extensos sobre dois apoios

Nestes casos, o corpo é sustentado por dois apoios. Para o sistema estar em equilíbrio, as forças seguem e satisfazem duas fórmulas, a primeira, a do equilíbrio vertical, já explicada anteriormente:

$\sum M_H=\sum M_{AH}\to F_1+F_2=F_A+F_B+F_C+...+F_n$

Onde:

• F₁ e F₂ são as forças dos apoios (momento de sustentação);
• F_A + F_B + F_C + ... + F_n são as forças em questão (momento de carga).

E a do equilíbrio de rotação, em que a soma dos momentos é equivalente entre a distância d dos apoios multiplicado pela força F do apoio. Todavia, as distâncias entre as forças e o apoio 1 é igual à distância multiplicada pela força do apoio 2:

$F_A{d}_A+F_B{d}_B+F_C{d}_C+...+F_n{d}_n=F_x{d}_x$

Onde:

• F é igual às forças de cada objeto, em newtons (N);
• d é a distância entre a força em questão e o apoio 1, em metros (m);
• F_x é a força do apoio 2, em newtons (N);
• d_x é a distância entre o apoio 1 e 2, em metros (m).

Demonstração

Em uma cidade do interior do estado do Mato Grosso, pretende-se construir uma ponte. Os engenheiros decidiram que a carga mínima (P) que a ponte deveria sustentar é de trinta toneladas. A ponte é sustentada por duas pilastras, A e B. Qual a carga sustentada por cada pilastra, sendo que a ponte tem cinco metros, sendo distância de um do outro exatamente cinco metros? Considere g = 10 m/s².

• Pelo equilíbrio de rotação, tem-se as seguintes distâncias e forças peso (observe que a distância da força de carga foi considerada 2,5 metros):

$300.000\times 2,5=F_A\times 5\to 750.000=5F_A\to F_A=150.000$

• E pelo equilíbrio vertical:

$F_A+F_B=P\to 150.000+F_B=300.000\to F_B=150.000$

Ou seja, cada pilastra sustenta, no mínimo, 150.000 N.