Logística/Localização/Localização em redes/Localização em redes em árvore/Localização de cobertura

O objectivo é localizar o menor número de novas instalações, em vários pontos de uma rede em árvore, de modo a que não seja ultrapassada uma certa distância $s_i$, entre cada nó $i$ da árvore e a instalação nova mais próxima. As novas instalações chamam-se centros. Esses centros prestam serviços, por exemplo, de abastecimento ou distribuição, aos nós da árvore, onde se localizam os clientes. As novas localizações podem ser localizadas em qualqeur ponto da árvore (Francis, 1992, p. 411-414).

Figura 9.12.1.3.1 Exemplo de resolução do algoritmo da Localização de Cobertura

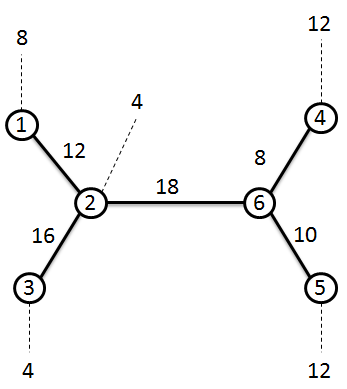
Considerando o exemplo da Figura 9.12.1.3.1, onde as linhas tracejadas ligadas aos nós de $1$ a $5$ representam os limites superiores das restrições de cobertura. Sendo assim, os valores de $s_i$ são os seguintes:

$s_1=8$

$s_2=4$

$s_3=4$

$s_4=12$

$s_5=15$

Para se poder dizer que um centro de distribuição cobre o nó $i$ da árvore a seguinte condição deve ser cumprida:

$d(x,v_i)\le s_i$

A resolução deste problema consiste em escolher uma das pontas da árvore, por exemplo $v_4$, como $s_4=12$ chega ao nó adjacente à ponta $v_6$ à distância de 8.

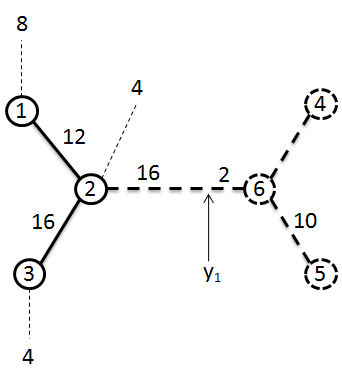
Após constatar que $s_4$ chega a $v_6$ pode-se remover o nó $v_4$, sendo que o novo valor de $s_4$ passa a ser $12-8=4$, estando a nova árvore representada na Figura 9.12.1.3.2.

Figura 9.12.1.3.2 Exemplo de resolução do algoritmo da Localização de Cobertura

O passo seguinte é a escolha de outra ponta da árvore, por exemplo $v_5$, constata-se que $s_5$ é maior que a distância ao nó adjacente $v_6$, pode-se assim remover $v_6$, isso faz com que existam dois valores para $s_6$, sendo então escolhido o menor, portanto $s_6$ passa a ser $s_6=2$. Dando o origem a uma nova árvore, representada na Figura 9.12.1.3.3.

Figura 9.12.1.3.3 Exemplo de resolução do algoritmo da Localização de Cobertura

No passo seguinte escolhe-se $v_6$, como $s_6=2$ não chega ao nó adjacente $v_2$, então, localiza-se um centro num ponto $y_1$ a uma distância 2 de $v_6$, de seguida remove-se todo o arco que liga $v_2$ a $v_6$, a nova árvore está representada na Figura 9.12.1.3.4.

Figura 9.12.1.3.4 Exemplo de resolução do algoritmo da Localização de Cobertura

Pode-se observar que $v_5$ é um nó distinto, dado que $y_1$ tem origem na restrição do nó $v_5$, então $u_1=\left\{v_5\right\}$, pode-se observar também que o novo centro apenas cobre os nós $v_4$, $v_5$ e $v_6$, com isto continua-se a analisar os restantes nós, por exemplo, analisa-se o nó $v_1$. Pode-se observar que $s_1=10$ o que não é suficiente para cobrir a distância de $v_1$ ao nó adjacente $v_2$, portanto regista-se um novo centro em $y_2$ e regista-se o facto de $v_1$ ser um nó distinto, ou seja, $u_2=\{v_5,v_1\}$. Observa-se que $s_2$ é suficiente para cobrir o novo centro $y_2$, portanto, podemos remover ambos os nós, dando origem a árvore representada na Figura 9.12.1.3.5.

Figura 9.12.1.3.5 Exemplo de resolução do algoritmo da Localização de Cobertura

Observando o nó $v_3$, pode-se ver que $s_3$ não é suficientemente grande para chegar ao nó adjacente $s_2$ nem suficientemente grande para atingir $y_1$ ou $y_2$, então, existe um novo centro de distribuição $y_3$ a uma distância de 4 do nó $v_3$, portanto o nó $v_3$ é um nó distinto, dando origem a $u_3=\{v_5,v_1,v_3\}$. A árvore resultante encontra-se representada na Figura 9.12.1.3.6.

Figura 9.12.1.3.6 Exemplo de resolução do algoritmo da Localização de Cobertura $u_3=\{v_5,v_1,v_3\}$

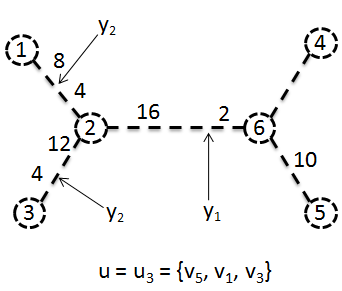
Sendo assim, pode-se dizer que para o exemplo referido a solução óptima consiste em três centros de distribuição, tendo os mesmos as seguintes localizações:

$y_1$ - Localizado no arco que liga $v_2$ a $v_6$, estando a uma distância de dois de $v_6$;

$y_2$ - Localizado no arco que liga $v_1$ a $v_2$, estando a uma distância de oito de $v_1$;

$y_3$ - Localizado no arco que liga $v_3$ a $v_2$, estando a uma distância de quatro de $v_3$.