Introdução à física/Equação das lentes

A equação das lentes é sempre:

$\frac{1}{f}=\frac{1}{p}+\frac{1}{p^{\prime }}$

em que os termos f, p e p' devem ser interpretados algebricamente.

p - por ser a lente simétrica, considera-se que p é sempre um número positivo (ou seja, o objeto está colocado no lado positivo do eixo horizontal)

f - a lente possui dois focos; considera-se que f é positivo para lentes convergentes e negativo para lentes divergentes

p' - como o objetivo primário de uma lente e fazer a imagem ser produzida do outro lado do objeto, então p' será positivo quando a imagem estiver do outro da lente em relação ao objeto (imagem real e invertida), e negativo caso contrário.

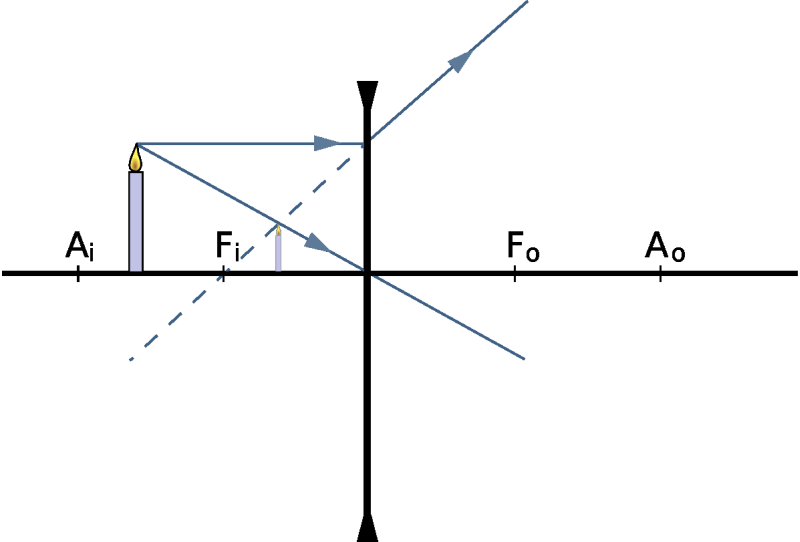
Lentes convergentes

Em uma lente convergente, seja f a distância focal, e p e p' , respectivamente, a distância do objeto à lente e a distância da imagem á lente. Por convenção, f é sempre um número positivo, e p e p' tem o mesmo sinal quando o objeto e a imagem estão colocados em lados opostos da lente (ou seja, temos uma imagem real e invertida).

Exemplos

• Lente com distância focal f = 15 cm e objeto colocado a p = 20 cm da lente. Então:

$\frac{1}{15}=\frac{1}{20}+\frac{1}{p^{\prime }}$

portanto p' = 60 cm

• Lente com distância focal f = 70 cm o objeto colocado a p = 50 cm da lente. Então:

$\frac{1}{70}=\frac{1}{50}+\frac{1}{p^{\prime }}$

portanto p' = -175 cm. Neste caso, a imagem está do mesmo lado do objeto, e é virtual e invertida.

Lentes divergentes

Predefinição:AutoCat