Matemática elementar/Geometria plana/Triângulos/Triângulo retângulo

Como dito anteriormente, um triângulo retângulo é aquele no qual um dos ângulos internos é reto.

Catetos e Hipotenusa

Em um triângulo retângulo, são chamados de catetos os lados perpendiculares entre si, ou seja, aqueles que formam o ângulo reto, e é chamado de hipotenusa o lado oposto ao ângulo reto.

Elementos de um triângulo retângulo. Os pontos A, B e C, os lados opostos a (hipotenusa), b e c (catetos) e as projeções de b e c, m e n.

A altura relativa à hipotenusa é o segmento de reta que parte do ponto onde está o ângulo reto e vai perpendicularmente até a hipotenusa.

As projeções dos catetos são as partes da hipotenusa divididas pela altura relativa.

Teorema de Pitágoras

Teorema de Pitágoras

Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

Seja $c$ a hipotenusa, sejam $a$ e $b$ catetos do mesmo triângulo:

$c^2=a^2+b^2$

Isso significa que, conhecendo as medidas de dois lados de um triângulo retângulo, pode-se calcular a medida do terceiro lado — propriedade única dos triângulos retângulos.

Demonstração do Teorema

Por semelhança

Existem várias formas de demonstrar o Teorema de Pitágoras. Esta demonstração é baseada na proporcionalidade de dois triângulos semelhantes.

Seja $ABC$ um triângulo retângulo, com o ângulo reto localizado em $C$, como mostrado na figura. Nós desenhamos o segmento de reta $h$ que passa por $C$ e é perpendicular a $\overline{AB}$. O novo triângulo $ACH$ é semelhante ao nosso triângulo $ABC$, pois ambos tem um ângulo reto (por definição de perpendicular), e eles compartilham o ângulo em $A$, implicando que o terceiro ângulo terá a mesma medida em ambos. De forma análoga, o triângulo $CBH$ também é semelhante a $ABC$. A semelhança leva a duas razões:

$\frac{\overline{AC}}{\overline{AB}}=\frac{\overline{AH}}{\overline{AC}}$

e

$\frac{\overline{CB}}{\overline{AB}}=\frac{\overline{HB}}{\overline{CB}}.$

Isto pode ser escrito como:

$\stackrel{2}{\stackrel{‾}{AC}}=\overline{AB}\times \overline{AH}$ e $\stackrel{2}{\stackrel{‾}{CB}}=\overline{AB}\times \overline{HB}.$

Somando as duas igualdades, obtemos:

$\stackrel{2}{\stackrel{‾}{AC}}+\stackrel{2}{\stackrel{‾}{CB}}=\overline{AB}\times \overline{AH}+\overline{AB}\times \overline{HB}=\overline{AB}\times (\overline{AH}+\overline{HB})=\stackrel{2}{\stackrel{‾}{AB}}.$

Em outras palavras, o Teorema de Pitágoras:

$\stackrel{2}{\stackrel{‾}{AC}}+\stackrel{2}{\stackrel{‾}{BC}}=\stackrel{2}{\stackrel{‾}{AB}}.$

Por equivalência de polígonos

Esta demonstração se baseia na congruência de triângulos e na equivalência de área de quadriláteros.

Dado $\mathrm{△}ABC$ retângulo em $B$ e seja $\overline{BH}$ a altura relativa à hipotenusa, marcamos na semi-reta $\overrightarrow{BH}$ um ponto $F$ tal que $\overline{HF}\cong \overline{AC}$ (lembre que $\overline{AC}$ é a hipotenusa). Então construímos o retângulo $AHFG$ (lembre que $\overline{AH}$ é a projeção de $\overline{AB}$).

Agora construímos $◻ABED$. A semi-reta $\overrightarrow{DE}$ intercepta $\overrightarrow{GA}$ em um ponto $I$, assim como $\overrightarrow{HB}$ em um ponto $J$. Temos o paralelogramo $ABJI$.

Como $◻ABED$ e $ABJI$ são paralelogramos de mesma base e mesma altura, ambos tem a mesma área.

Por definição de quadrado, segue que $\overline{AD}\cong \overline{AB}$, e também $\mathrm{\angle }ADE$ é reto. Portanto, $\mathrm{\angle }ADE\cong \mathrm{\angle }ABC$.

$\mathrm{\angle }DAI$ e $\mathrm{\angle }BAC$ são ambos suplementares de $\mathrm{\angle }IAB$. Portanto, $\mathrm{\angle }DAI\cong \mathrm{\angle }BAC$.

Segue pelo critério lado-ângulo-ângulo de congruência de triângulos que $\mathrm{△}ABC\cong \mathrm{△}ADI$. Portanto, $\overline{AI}\cong \overline{AC}$, e por extensão, $\overline{AI}\cong \overline{HF}$.

Como $ABJI$ e $AHGFI$ são paralelogramos de mesma base e mesma altura, ambos tem a mesma área. Ou seja, a área do quadrado sobre um cateto é igual à área do retângulo determinado pela projeção deste cateto e um segmento congruente à hipotenusa. Como a união do retângulo determinado por $\overline{AH}$ e $\overline{HF}$ com o retângulo determinado por $\overline{HC}$ e $\overline{HF}$ é igual ao quadrado sobre $\overline{AC}$, segue que a soma das áreas dos quadrados sobre os catetos é igual a área do quadrado sobre a hipotenusa.

Q.E.D.

Aplicações do Teorema

Com o teorema de Pitágoras, pode-se calcular o comprimento da hipotenusa de um triângulo conhecendo apenas o comprimento de cada cateto deste. Ou ainda, calcular o comprimento de um cateto conhecendo apenas a medida da hipotenusa e de outro cateto. O teorema de Pitágoras pode também ser usado para calcular o comprimento da diagonal de um retângulo conhecendo apenas os lados deste.

Exemplos

• Seja $ABC$ um triângulo retângulo no qual $\overline{AB}$ consista em um dos catetos o qual mede 3 metros de comprimento e $\overline{AC}$ consista em outro cateto o qual mede 4 metros de comprimento. Calcule o comprimento da hipotenusa $\overline{BC}$.

• • Resolução

Dado o Teorema de Pitágoras, $\stackrel{2}{\stackrel{‾}{BC}}=\stackrel{2}{\stackrel{‾}{AB}}+\stackrel{2}{\stackrel{‾}{AC}}$, tem-se que $\overline{AB}=3$ e $\overline{AC}=4$, portanto:

$\stackrel{2}{\stackrel{‾}{BC}}=3^2+4^2$

$\stackrel{2}{\stackrel{‾}{BC}}=9+16$

$\stackrel{2}{\stackrel{‾}{BC}}=25$

$\sqrt{\stackrel{2}{\stackrel{‾}{BC}}}=\sqrt{25}$

$\overline{BC}=5$

A hipotenusa do triângulo $ABC$ mede 5 metros.

• Um triângulo retângulo tem os lados $a$, $b$ e $c$, sendo que $a$ é um cateto e mede 1 centímetro de comprimento, enquanto $c$ é a hipotenusa e mede 2 centímetros. Calcule o comprimento do cateto $b$

• • Resolução

Dado o Teorema de Pitágoras, $c^2=a^2+b^2$, tem-se que $a=1$ e $c=2$, portanto:

$2^2=1^2+b^2$

$4=1+b^2$

$4-1=1+b^2-1$

$3=b^2$

$\sqrt{3}=\sqrt{b^2}$

$b=\sqrt{3}$

O cateto $b$ mede $\sqrt{3}$ centímetros de comprimento.

Triângulos retângulo notáveis

Triângulo 3_4_5

Prova visual para o triângulo (3, 4, 5), Chou Pei Suan Ching 500–200 d.C.

Um "triângulo 3_4_5" é qualquer triângulo retângulo que tenha esta proporção de lados. Ou seja, um triângulo cujo um dos catetos tem o comprimento $l_1$, outro cateto, o comprimento $l_2$ e a hipotenusa, $l_3$; tal que haja um número $n$ que:

$\frac{l_1}{n}=3$

$\frac{l_2}{n}=4$

$\frac{l_3}{n}=5$

A consciência desta proporção permite, a partir do comprimento de dois lados de um triângulo 3_4_5, inferir rapidamente o comprimento do terceiro lado. Por exemplo, sabendo que um triângulo tem um lado de 6 metros e outro de 8 metros, pode-se inferir corretamente que o outro lado tem 10 metros (onde n=2).

Triângulo 45º_45º_90º

O chamado "triângulo 45º_45º_90º" possui ângulos com essas medidas e a proporção entre seus lados é: $1:1:\sqrt{2}$. Ou seja, um triângulo retângulo e isóceles.

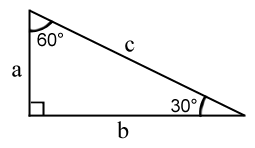
Triângulo 20º_70º_90º

O "triângulo 30º_60º_90º" possui ângulos com essas medidas e a proporção de seus lados é: $1:\sqrt{3}:2$.

Exercícios resolvidos

Na comédia antiga Diálogo dos mortos, do poeta satírico Predefinição:W, Predefinição:W empilha as montanhas Ossa e Pelion sobre o Olimpo, na esperança de, a partir de um ponto de vista mais alto, poder mostrar toda a Terra para Predefinição:W; para sua decepção, porém, ele só consegue ver ao oeste, parte da Itália, ao sul, até Creta, ao leste, até a Jônia e, ao norte, até o Danúbio. Considerando a Terra esférica, que a visão corresponde a um raio tangente, que o ponto mais distante observado seja o ponto de tangência, que a soma da altura dos três montes seja 5 km e que a distância até o ponto de tangência seja 400 km, calcule qual foi o raio da Terra usado por Luciano.

Ver também

• Trigonometria
• Lei dos senos e dos cossenos
• Demonstração ilustrada do Teorema de Pitágoras na edição de Byrne dos Elementos de Euclides